Synchronous Generator Transients

Hello friends, I hope all of you are fine. In today’s tutorial, we are gonna have a look at synchronous Generator Transients. The synchronous generator is also known alternator that transforms mechanical energy that is provided by its prime mover at shaft into electrical energy at specific voltage and frequency. Its rotation speed is known as synchronous speed because its rotation speed equals the speed of rotation of field at stator that known as synchronous speed.

Due to this, it used in such an application where constant speed is essential. It mostly used in our generation structure for the creation of energy. In today’s post, we will have a look at its transients and their effect on the working of the synchronous generator. So let’s get started with Synchronous Generator Transients.

Synchronous Generator Transients

• When the torque provided to the shaft of the synchronous generator by the prime mover or the load connected with the generator varies abruptly, then transients produce in the generator that will remain until the generator again gets the stability.

• For instance, when the generator is connected in parallel with the already working power system, as we discussed in Parallel Operation of Synchronous Generator that the incoming generator frequency should be higher than the running system, so its frequency is larger than the system.
• When a generator is paralleled, there are transient’s intervals before it works steadily and starts to operate at the frequency equal to the system.
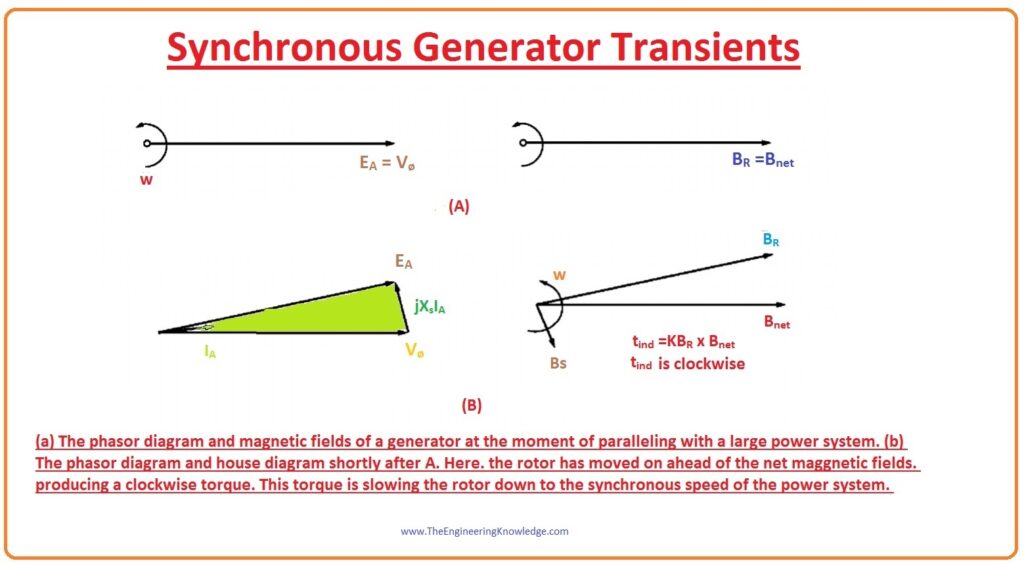
• To discuss this condition let’s see the given diagram.
• In the diagram that is denoted as A, explains the magnetic field and the phasor diagram of the generator at the instant just before it connected with the power system.
• At that moment incoming generator providing no power to the load and its stator current is also 0.
• As there is no load connected with the generator its internal generated voltage E_A will equal to the output voltage V_ø, E_A = V_ø and field will equal to the net field, B_R =B_net
• At the time of paralleling when the generator is connected with the system, then stator current starts to flow through the generator.
• As the rotor of the generator is still rotating faster than the system’s speed, it lasts to move out ahead of the voltage of the system V_ø.

• The torque produced on the generator’s shaft is given as.

t_ind =KB_R x B_net

• The direction of the rotation of this torque is opposite to the rotation of the generator’s rotor. It is directly proportional to the angle between the rotor field B_R and the net field B_net.
• As the direction of the torque is opposite to the direction of the rotation of the generator so it stops the generator then a generator starts to move at synchronous speed with the power system.
• Correspondingly, if the generator was rotating at a speed lesser than synchronous speed when it was connected in parallel with the power system then the rotor will fall behind the B_net and torque produced in the direction of motion will produced on the rotor of the generator.
• Due to this torque, the rotor starts to move at the synchronous speed.

Transient Stability of Synchronous Generators

• As we know that the extreme power that a generator can provide to its load at any condition is known as the static stability limit of a synchronous generator.
• The maximum power that a generator can provide to load is given here.

P_max = 3V_øE_A/X_s

• And the maximum torque of the synchronous generator is given here.

t_max = 3V_øE_A/wX_s

• Theoretically, the generator should provide torque and the power to that above-given quantity before becoming unbalanced.
• But practically due to the dynamic stability boundary the extreme power that can be provided by the generator is restricted to a lesser level.
• To find the reason of these restrictions we analyze the above-given diagram of the generator.
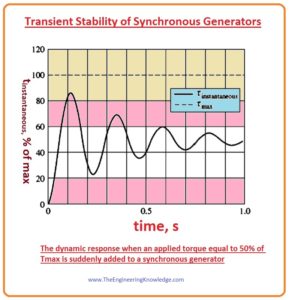
• If the torque provided t_app by the prime mover of the generator is abruptly increased, the shaft of the generator will start to move fastly and the angle of the torque will also increase.
• Due to the increment in angle the induced torque t_ind will also increase till that point of angle then the torque induced is identical and opposite in direction to the applied torque t_app.
• It is the steady-state working point of the generator with the new load.
• Though the generator has the ability of inertia, therefore its torque angle (δ) truly exceeds the steady-state situation and slowly settles out in a damped oscillation. It shows in a given diagram.

• The significant point above diagram is that if at any point in the transient response the instantaneous torque surpasses T_max, the generator will lose its stability.
• The amplitude of the oscillations relies on how abruptly the extra torque provided to the generator.
• If torque is provided very slowly, the generator has the ability nearly reach the static stability limit.

• If the load is connected abruptly with the generator, the generator will be steady only to a very lesser limit, it is very complex to measure.
• Foreach sudden variations in torque or load, the dynamic stability limit can be less than half of the static stability limit.

Short-Circuit Transients in Synchronous Generators

• The most dangerous transient situation that can occur in a synchronous generator is the point when the 3 phases of the generators are connected with each other. This type of connection (short circuit) among three phases is known as the fault.
• There are numerous mechanisms of current present in a short-circuited synchronous generator, that are defined here.
• The similar facts occur in less dangerous transients like load variation, but they are very understandable in the dangerous case of a short-circuit.
• When the terminals of the generator are short-circuited, the resultant current flowing the 3 phases of the generator is shown in a given diagram.

Before the fault, only ac voltages and currents were present within the generator, while after the fault, both ac and dc currents are present. Where did the dc currents come from? sub

• One thing keeps in mind that the synchronous generator is an inductive load, its internal generated voltage E_A is in series with the synchronous reactance X_s.
• Also, remember that the current cannot vary immediately in an inductive load (inductor).
• When the faults occur on generator alternating current components move to larger value, while the total current remains the same.
• The direct current components of the current are larger enough that addition of the alternating current and the direct current components just after the short circuit equivalent to the alternating current moving just before short-circuited (fault).
• These direct current components of current falling-off very rapidly, but at start, they are fifty to sixty percent of the alternating current flowing at the point just after the short circuit (fault).
• The over-all preliminary current is therefore characteristically 1.5 or 1.6 times the alternating current component taken alone.
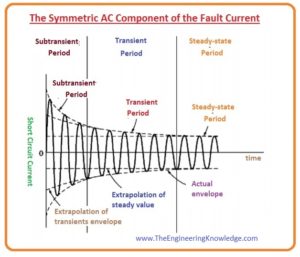
• The pictorial representation of the alternating current symmetrical component of current is shown here.

• The alternating current components are divided into the 3 main time periods. after the short circuit (fault) occurrence you can see that the alternating current amplitude is very high, and its decays very fastly. This interval is known as the sub transients
• After the sub transients period the large amplitude of the current continues to decay slowly, finally it get steady state.

• The time interval in which the amplitude of the current decay slowly is known as a transient period and interval then it gets steady-state condition is called steady state period.
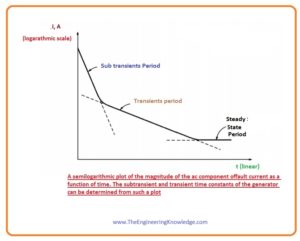
• If we construct thee root mean square magnitude of the alternating current as function of the time, then we can easily understand the 3-time intervals of the fault current. It shows in given diagram.
• It is likely (possible) to find the time constants of the declines in every time interval from this graph.

• The root means square alternating current passing through the generator during sub transients time interval is known as the sub transient current and it represented as the I’’.
• To removal this current we use damper winding in the synchronous current.
• The time constant of the sub transient current is denoted as the T’’ and its value can be measured by the slop of the sub transients current in above given figure,
• The value of this current can be ten time the value of the steady-state fault current.
• The root means square current passing in the generator in the transient time interval is known as the transients current and represented as I’.
• It is produced by a direct current component of current produced in the field circuitry of a generator when a short circuit occurs.
• Due to this field current, there is an increase in the internal generated voltage E_A that upsurges the short circuit (faults) current.
• As the time constant of the direct current field circuitry is larger than the time constant of the damper windings, due to this the time interval of the transient is larger than the sub transient interval.
• This constant of time is denoted as the T’.
• The average root mean square current during the transient interval is five-time the steady-state short (fault) circuit current.
• With the finishing of the transient interval, the short circuit current follows the steady-state condition.
• The steady-state current during a short circuit is represented as I_ss.
• It is given almost by the fundamental frequency constituent of the E_A and the synchronous reactance Xs.

I_ss = E_A/ X_s

• The root means square amplitude of the alternating fault current in generator changes continuously as function the T.
• If I’’ is the sub transient constituent of current at the time of the short circuit, I’ is the transient constituent of current at the time of the short circuit and I_ss is the steady-state short (fault) current then the root mean square magnitude of the current at any time after a short circuit (fault) at the output terminals of the generator is given as.

I(t) = (I’’ -I’)e^-t/T” + (I’ – 1_ss)^e-t/T’ + I_ss

• It is usual to describe sub transient and transient reactance’s for a synchronous generator as an appropriate way to define the sub transient and transient elements of short circuit (fault) current.
• The sub transient’s reactance of synchronous generator can be described as it is the ratio of the E_A to the sub transient element of current at the start of short circuit current.

X’’ = E_A/I’’ sub transient

• Correspondingly, the transient’s reactance of generator can be defined as it the ratio of the E_A to the transient’s element of the current I’ at the start of the short circuit (fault.)

X’ = E_A/I’ transients

You can also read some related topics to synchronous generator that are listed here.

Introduction to Synchronous Generator

Synchronous Generator Equivalent Circuit  

Synchronous Generator Phasor Diagram

Synchronous Generator Power and Torque

Synchronous Generator Parameters

Synchronous Generator Operating Alone

Synchronous Generator Parallel Operation

Synchronous Generator parallel with Large Power system

Synchronous Generator Parallel with same Size Generator

Synchronous Generator Ratings

Synchronous Generator Capability Curves

This is the detailed article on Synchronous Generator Transients each and every fact related to Synchronous Generator Transients have been mentioned in this post. If you still have any query please ask in comments. I will resolve your problems. See you in the next tutorial Frequency-Power and Voltage-Reactive Power Characteristics of a Synchronous Generator.