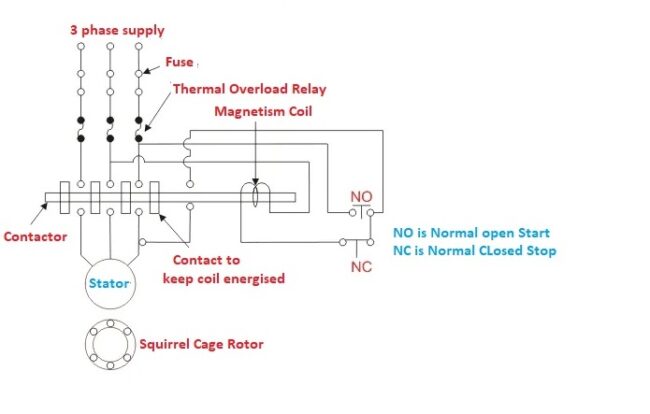
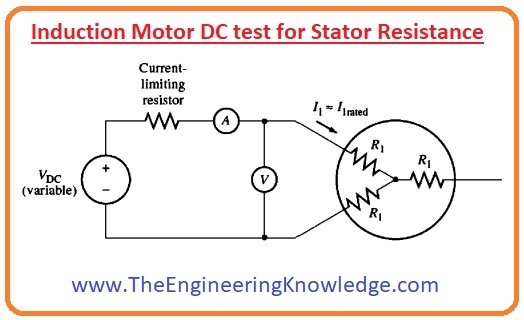
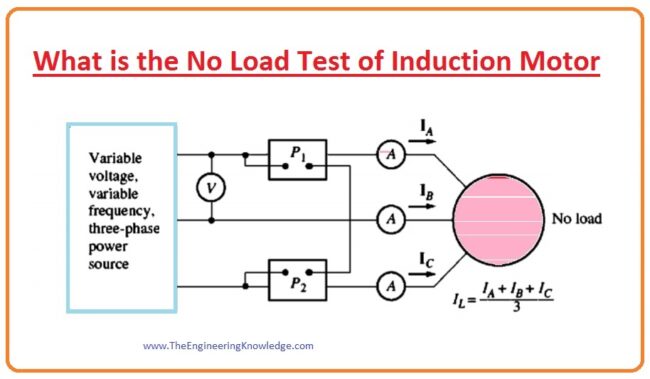
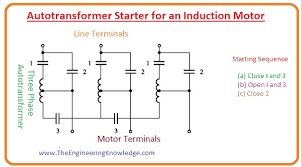
Introduction to DOL Starter (Direct On Line Starter)
Hello, readers welcome to the new post. In this post, we will discuss the Introduction to DOL Starter (Direct On Line Starter). The induction motor takes a larger amount of current at the start. This high current is harmful to the windings of the motor. There are different methods used to save windings from the…