What is the Maximum (Pullout) Torque in an Induction Motor

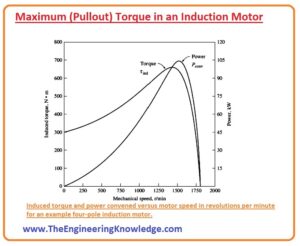
Hello friends, I hope all of you are doing great. In today’s tutorial, we are gonna have a look at the Maximum (Pullout) Torque in an Induction Motor. The maximum or pull-out torque of the three-phase induction motor three-phase induction motor is the extremely bearable torque that the motor can produce without any sudden decrease in its regular speed but for a short time interval. If the motor stays working at its maximum or pullout torque, it will produce serious damage to the rotor of the motor, and in conclusion, the speed of the motor will steadily slow down and the motor stops to work.

In today’s post, we will have a look at how torque is produced in the motor and its facts. So, let’s get started with the What is the Maximum (Pullout) Torque in an Induction Motor?

What is the Maximum (Pullout) Torque in an Induction Motor

• As we have discussed in the previous article that the induced torque in the induction motor is found by this equation.

T_ind = P_AG/W_sync

• The maximum (pullout) probable torque exists when the air-gap power (P_AG) is extreme. As the air-gap power (P_AG) is equivalent to the power spent in the resistance (R2 /s), the maximum (pullout) induced torque will arise when the power loss by that resistance is extreme.

• As we can see in the given circuit diagram, if we apply the maximum power transformer theorem to this circuit, the maximum power transfer theorem says that the maximum (extreme) power transmitted to the output (in this circuit the output is (R₂/s) ) if the impedance (Z) at the output equals to the impedance at the input.
• The correspondent source impedance (Z) in the circuitry is given as.

Z_source = R_TH + jX_TH + jX₂

• Thus, the maximum transfer of power will exit when the given below equation we get.

R₂/s = √(R2_TH + (X_TH + X₂)²)

• By resolving this equation, we can find the value of slip at the maximum (pullout) torque of the induction motor which is given below.

S_max = R₂/√(R²_TH + (X_TH + X₂)²)

• From this equation, you can note that rotor resistor (R₂₎ exits at the numerator of this equation, thus at maximum (pullout) torque slip (S) of the rotor is directly proportionate to the resistance (R₂) of the rotor.
• To find the equation of extreme torque we put the slip equation in the given expression.

T_ind= (3V_THR₂/s)/ W_sync[(R_TH+R₂/s)²+(X_TH+X₂)²]

• This induced torque equation we have determined in the last article which is Derivation of the Induction Motor Induced-Torque Equation you can read it to get this expression.
• After putting the slip equation in the induced torque equation get the expression of the maximum torque.

T_max = 3V²_th/(2w_sync[R_TH +√(R²_TH + (X_TH + X₂)²)]

• From this equation, we can see that the maximum torque of the induction motor is proportionate to the square of the input voltage (V) and inversely proportionate to the impedance of the rotor and the reactance of the rotor.
• If the motor has a smaller value of reactance, then it will have a large amount of maximum torque.

• From the slip equation, we can observe that the slip at which maximum torque exits is directly proportionate to the resistance of rotor, but from the maximum torque equation we can see that the maximum torque does not depend on the value of the resistance of the rotor.

 

 

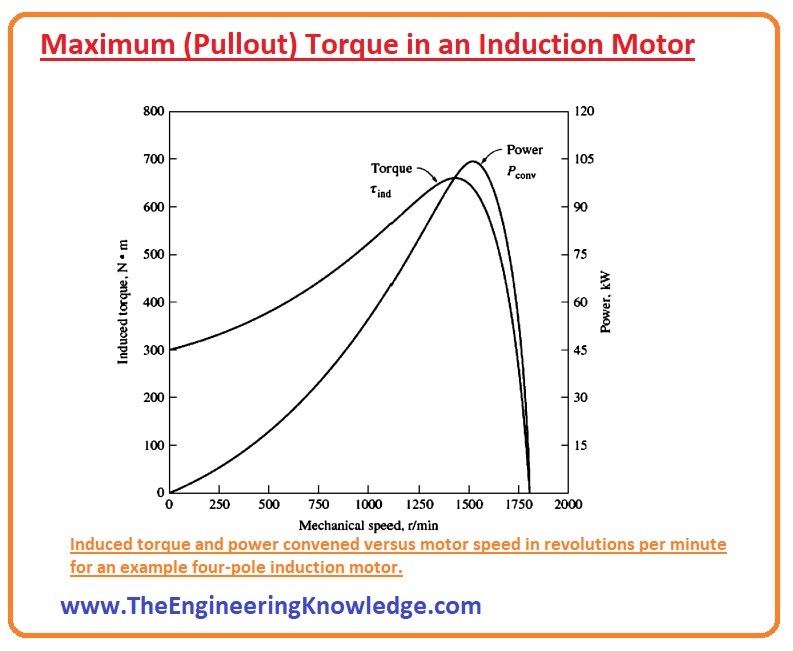
Effect of varying rotor resistance on the torque-speed characteristic of a wound-rotor induction motor

• The torque-speed characteristic curve for a wound rotor induction motor is drawn in the given diagram.
• Remember that it is feasible to add resistance into the rotor circuitry of a wound rotor as the rotor circuitry is brought out to the stator over slip rings.

• You can note from the diagram that as the resistance of the rotor upsurges the pullout speed of the motor declines, but the maximum (pullout) torque does not vary.
• It is likely to take benefit of this characteristic of wound-rotor induction motors to start very weighty loads.
• If resistance is added to the rotor circuitry, the maximum (pullout) torque can be set to exit at initial situations.
• So, the maximum conceivable torque would be accessible to start weighty loads.
• On the other hand, when the load is rotating, the additional resistance can be detached from the circuitry, and the maximum (pullout) torque will transfer to near-synchronous speed (w_sync) for the steady process.

So, friends, it is all about the Maximum (Pullout) Torque in an Induction Motor, if you want to know something else about it ask in the comments. Thanks for reading. See you in the next tutorial.

You can also read some related articles to the induction motor. That is described here.

• Introduction to Induction Motor
• Introduction to Three Phase Induction Motor
• Equivalent Circuit Induction Motor
• Induction Motor Torque-Speed Characteristics
• Variations in Induction Motor Torque-Speed Characteristics
• Power and Torque in Induction Motors
• Induction Motor Design Classes
• speed Control Method of Induction Motors
• Induction Motor Design
• No-load Test of Induction Motor
• Solid State Drive Induction Motor
• Derivation of the Induction Motor Induced-Torque Equation
• Induction Motor Induced-Torque Equation

Faqs

1. What is the maximum torque in an induction motor?

The maximum torque in an induction motor is the maximum torque that the motor can generate at a given slip. It is also called the pullout torque. The maximum torque caused when the air-gap power is maximum. it occurs when the rotor resistance is like the rotor reactance.

2. What is the difference between maximum torque and full load torque?

The maximum torque is the maximum torque that the motor can generate at any speed. The full load torque is the torque that the motor can generate at its rated speed. The full load torque is normally about 70% of the maximum torque.

3. What factors affect the maximum torque of an induction motor?

The maximum torque of an induction motor is affected by these parameters

• Rotor resistance: The higher the rotor resistance, the higher the maximum torque.
• Rotor reactance: The lower the rotor reactance, the higher the maximum torque.
• Supply voltage: The high the supply voltage, the higher the maximum torque.
• Motor size: The larger the motor, the higher the maximum torque.

4. How can I increase the maximum torque of an induction motor?

There are some techniques to increase the maximum torque of an induction motor:

• Increase the rotor resistance: it can be done by adding external resistance to the rotor circuit.
• Reduce the rotor reactance: it is done by using a motor with a high-frequency supply.
• Increase the supply voltage: it increases the maximum torque, but it will also increase the current draw of the motor.
• Use a larger motor: it increases the maximum torque, but it will also increase the prices of the motor.

5. What happens if the load torque exceeds the maximum torque of the induction motor?

If the load torque is larger than the maximum torque of the induction motor, the motor will stall. it shows that the motor will stop rotating and the current will increase to high value. it can damage the motor if it is not shut down quickly.

6. How can I protect an induction motor from stalling?

There are some methods to protect an induction motor from stalling:

• Use a starter that limits the inrush current: It will prevent the motor from overloading and stalling.
• Use a soft starter: it gradually increases the motor speed, which will help to avoid stalling.
• Use a current limiter: This will shut down the motor if the current is larger than a certain level.

7. What is the difference between pullout torque and breakdown torque?

The pullout torque is the maximum torque that the motor can generate without losing synchronism with the supply voltage. The breakdown torque is the maximum torque that the motor generates before it stalls. The breakdown torque is slightly higher than the pullout torque.

8. What is the significance of maximum torque in an induction motor?

The maximum torque is one main feature of an induction motor. It is the maximum torque that the motor can generate, which is important for applications where the motor needs to start heavy loads. The maximum torque is good for applications where the motor needs to operate at variable speeds.

9. How is maximum torque measured in an induction motor?

The maximum torque of an induction motor is calculated with a torque meter. The torque meter is attached to the motor shaft and the load is slowly increased until the motor stalls. The torque at which the motor stalls is the maximum torque.

10. What are the applications of maximum torque in an induction motor?

The maximum torque of an induction motor is used in different applications

• Starting heavy loads: The maximum torque is used to start motors that have a high inertia load, such as fans, pumps, and conveyors.
• Operating at variable speeds: The maximum torque is used to operate motors at variable speeds, such as in wind turbines and elevators.
• Controlling the position of machines: The maximum torque is used to control the position of machines, such as in robots and machine tools.