Hello, readers welcome to the new post. In this post, we will have a detailed look at Balanced Three-Phase Circuits Power. The system that has the same values of all three phases for voltage and phase angle of one twenty degrees is called a balanced three-phase system.
In this post, we will determine how to finds the power of a balanced three-phase system and discuss its different parameters. So let get started with Balanced Three-Phase Circuits Power
Balanced Three-Phase Circuits Power
- The power generated by the three-phase generator or used by the load connected to the generator is the sum of power existing in the three phases.
- In the balanced system, it is multiple of three as the same power is flowing in phases
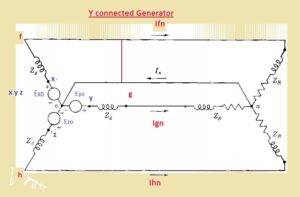
- If the value of voltage to neutral is denoted Vp in case of the load is liked in Y connection arranges. then we have
- Vp=Vxn=Vyn=Vzn
- Here X, y z are three phases
- If the current flowing in the Y connection is IP then we have
- Ip=Ixn=Iyn=Izn
- the net power flowing in the system we have
- P=3VpIpcosθp
- Here θp is the value of angle through current ip lags behinds the Vp
- this angle also denoted the angle of imp for any phase
- If ΙVLΙ and IILl is the magnitude of line-to-line voltages and IL is line current then we have.
- ΙVpΙ=ΙVLΙ/√3 and IILl is equal to lIPl
So the power will be
p=√3ΙVLΙlILlcosθp
Value for reactive power will be
Q=3ΙVpΙlIplsinθp
p=√3ΙVLΙlILlsinθp
- Volamper equation will be
- lSl=√p^2+Q^2=√3lVLllILl
- So these equations are used to find the power of three-phase ac system that is balanced
- If the load is configured in delta arrangement the voltage about every impedance is line to line voltage and magnitude of current in every impedance is the magnitude of line current divided by√3
- lVpl=lVLl and lIpl=lILl/√3
- Sot the net power in the delta system will be
- P=√3lVLllILlcosθp
That is all about the Balanced Three-Phase Circuits Power if you have any further query ask in comment. See you in enxt post
