The concept of limits was initially introduced by the Greek mathematician Archimedes of Syracuse (287–212 BC) to compute the volume of a sphere and curved shapes. The goal is to break these numbers down into manageable bits so that they can be calculated. When the number of pieces grows, the needed amount will also grow as well, up to the limit of the sum of all the pieces.
The fundamental concept of limit in calculus sometimes embodies the idea of arbitrary nearest. A limit is when a variable quantity gets as close as possible to the desired value. The majority of calculus derivative and integral operations are based on limit theory. Furthermore, in this article, the basic idea of the limit with its definition, formula, and with the help of
examples topic will be explained.
Definition:
“Limit value of some function is an input which will meet some value as possible it can”
The limit of a function is written as:
Rules for Limit:
In this section with the help of rules, the topic will be explained
Addition Rule:
The addition rule tells us that if you have a sum of two function limits then it is equal to the sum of their
limits. Like, if Lim y → c (g(y)) = K and Lim y → c (f(y)) = L, then
Lim y →c [g(y) + f(y)] = K + L
Constant Rule
The constant function limiting value is similar to that of the constant itself. Let’s suppose "k" is a constant, then
Lim y →c (k) = k
Difference Rule:
The difference rule tells us that if you have a difference between two function limits then it is equal to the difference between their limits. Like, if Lim y → c (g(y)) = K and Lim y → c (f(y)) = L, then
Lim y→c [g(y) – f(y)] = K – L.
Product Rule:
The Product rule tells us that the limit of the product of two is equal to the product of their limits. If Lim y→c
(g(y)) = K and Lim y→c (f(y)) = L, then Lim y→c [g(y) f(y)] = KL
Example Section:
Example 1:
Calculate the limit of 3y 4 – 16y 3 + 12y 2 + 3y – 16, where y approaches 2.
Solution:
Step 1:
Using limits in the given function
f(y) = 3y 4 – 16y 3 + 12y 2 + 3y – 16
c = 2
Lim y→c f(y) = Lim y→2 (3y 4 – 16y 3 + 12y 2 + 3y – 16)
Step 2:
Applying the limits notation separately by using the rules of the limits mentioned in the above table.
Lim y→2 (3y 4 – 16y 3 + 12y 2 + 3y – 16) = Lim y→2 (3y 4 ) – Lim y→2 (16y 3 ) + Lim y→2 (12y 2 ) + Lim y→2 (3y) – Lim y→2 (16)
Step 3:
Write the constants outside the limit using the constant multiplication rule.
Lim y→2 (3y 4 – 16y 3 + 12y 2 + 3y – 16) = 3 Lim y→2 (y 4 ) – 16 Lim y→2 (y 3 ) + 12 Lim y→2 (y 2 ) +3 Lim y→2 (y) – Lim y→2 (16)
Step 4:
Replacing limit value with y.
Lim y→2 (3y 4 – 16y 3 + 12y 2 + 3y – 16) = 3(2 4 ) – 16 (2 3 ) + 12 (2 2 ) + 3 (2) – 16
Lim y→2 (3y 4 – 16y 3 + 12y 2 + 3y – 16) = 3 (2 * 2 * 2 * 2) – 16 (2 * 2* 2) + 12 (2 * 2) + 6 – 16
Lim y→2 (3y 4 – 16y 3 + 12y 2 + 3y – 16) = 3(16) – 16(8) + 12(4) + 6 – 16
Lim y→2 (3y 4 – 16y 3 + 12y 2 + 3y – 16) = 48 –128 + 48 – 10
Lim y→2 (3y 4 – 16y 3 + 12y 2 + 3y – 16) = 96 -128 -10
Lim y→2 (3y 4 – 16y 3 + 12y 2 + 3y – 16) = – 32 -10
Lim y→2 (3y 4 – 16y 3 + 12y 2 + 3y – 16) = – 42
(3y 4 – 16y 3 + 12y 2 + 3y – 16) = – 42
Example 2:
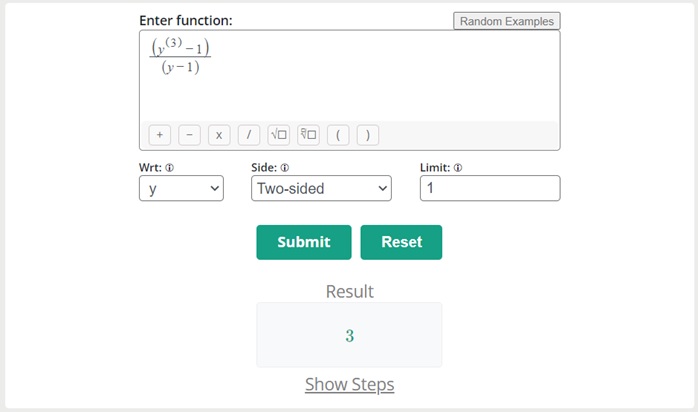
Calculate the limit of the function f(y) = (y 3 – 1) / y – 1 where y approaches 1.
Solution:
Step 1:
Putting the limits in the given function
f(y) = (y 3 – 1) / (y – 1)
c = 1
Lim y→1 f(y) = Lim y→1 (y 3 – 1) / (y – 1) = {Lim y→1 (y 3 ) – Lim y→1 (1)} / {Lim y→1 (y) – Lim y→1 (1)}
Lim y→1 (y 3 – 1) / (y – 1) = (1 3 ) –1)} / {(1) – (1)}
Lim y→1 (y 3 – 1) / (y – 1) = 0 / 0
Which is an indeterminate form
Step 2:
Now converting it into a reducible form
Lim y→1 (y 3 – 1) / (y – 1) = Lim y→1 {(y-1) (y 2 +y+1) / (y-1)}
Canceling the like terms
Lim y→1 (y 3 – 1) / (y – 1) = Lim y→1 (y 2 + y + 1)
Step 4:
Now putting a limit on the reducible function
Lim y→1 (y 3 – 1) / (y – 1) = Lim y→1 (y 2 + y + 1)
Lim y→1 (y 3 – 1) / (y – 1) = 1 2 + 1 + 1
Lim y→1 (y 3 – 1) / (y – 1) = 1 + 1 + 1
Lim y→1 (y 3 – 1) / (y – 1) = 3
Try online tools to cross check the results of limit problems.
Solved through limits calculator
Solved through limits calculator
Example 3:
Evaluate the limit of the function lim x→0 Sin(x)/x
Solution:
Step 1:
Putting the limits in the given function
F(x) = lim x→0 F(x) = lim x→0 Sin (x)/x
Lim x→0 F(x) = Sin (0) /0
Lim x→0 F(x) = 0/0
Which is an indeterminate form
Step 2:
To make it in determinate form apply the L’ Hospital rule by taking the derivative of the numerator and
denominator
Lim x→0 F(x) = lim x→0 d/dx Sin (x) /d/dx (x)
lim x→0 F(x) = lim x→0 cos (x) / 1
lim x→0 F(x) = lim x→0 cos (x)
Step 3:
Now putting a limit on it
lim x→0 F(x) = cos (0)
Lim x→0 F(x) = 1
Summary
In this article, you have learned about the basic of limit definition, formula, and different rules used to make it easier, and then for better understanding with the help of examples, the topic is explained. Moreover, after understanding and practicing one or more examples given in this article anyone can easily defend this topic.