 Hello, friends, I hope you all are enjoying your life. In today’s post, we will have a detailed look at the Operation of LC Feedback Oscillators. Generally, the RC feedback oscillator which also called Wien Bridge is normally used for frequency value close to the one megahertz. LC feedback components are generally used in oscillators which need a large value of frequencies with oscillation. Due to the frequency restriction of mostly operational amplifier separate transistors such as BJT or field-effect transistor are used as a gain component in the circuit of LC oscillator.
Hello, friends, I hope you all are enjoying your life. In today’s post, we will have a detailed look at the Operation of LC Feedback Oscillators. Generally, the RC feedback oscillator which also called Wien Bridge is normally used for frequency value close to the one megahertz. LC feedback components are generally used in oscillators which need a large value of frequencies with oscillation. Due to the frequency restriction of mostly operational amplifier separate transistors such as BJT or field-effect transistor are used as a gain component in the circuit of LC oscillator.
In this post, we will discuss about the circuit and operation of LC Feedback oscillator. So let’s get started with Operation of LC Feedback Oscillators.
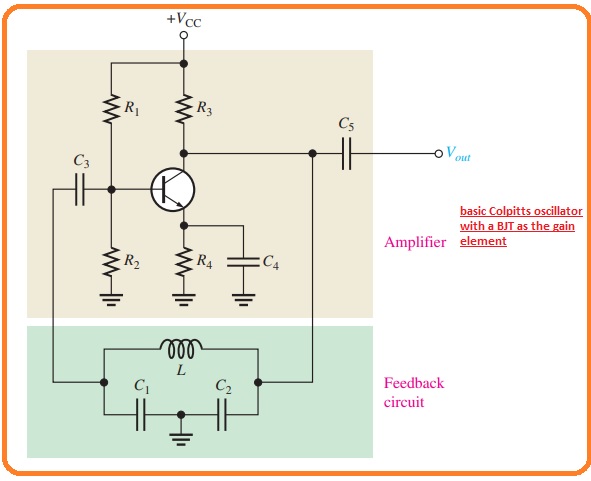
What is Colpitts Oscillator
- The main category of resonant circuitry feedback oscillator is Clopitts its name is due to its creator. It can be seen in below figure.
- This category of oscillator used in LC circuitry in the feedback loop to deliver the compulsory phase shift and to work like a resonant filter which allows to pass only required frequency of oscillation.
- The closet value of frequency of oscillation is the resonant frequency of the LC circuitry and is maintained by the values of capacitors C1, C2, and inductor L according to this below expression.
fr=1/2π√LCT
- In this equation the total capacitance is CT. since the capacitor effectively exists in series with the tank circuitry the value of total capacitance is given here.
CT =C1C2/(C1+C2)
Conditions for Oscillation and Start-Up
- The attenuation B is the resonant feedback circuitry in the Colpitts oscillator is generally find with the value of capacitor C1 and C2.
- The below figure indicates that the circulating tank current is passing through the capacitor C1 and C2.
- The voltage generated about the oscillator output voltage and voltage created about the feedback voltage is denoted as.
- The relation for attenuation B is given as.
- B = Vf/Vout=IXC1/IXC2=XC1/XC2=1/(2πfrC1)/(1/(2πfrC2))
- After simplifying we have
B = C2/C1
- As we know that conditions for oscillation AvB is one. Hence B=C2/C1
Av=C1/C2
- Here the voltage gain of amplifier that is denoted with the triangle is shown in the below figure.
- 16-17
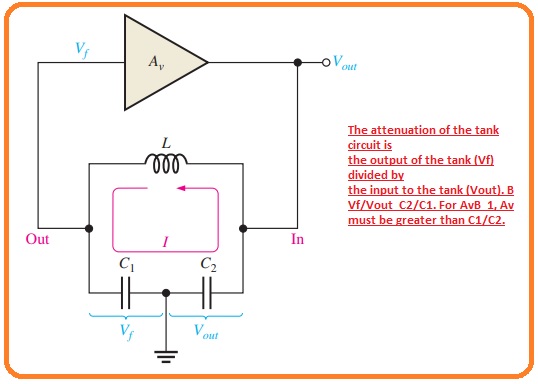
- According to this situation AvB = (C1/C2)(C2/C1) = 1. In reality for the oscillator is self-starting should be larger than one.
Av>C1/C2
Loading of the Feedback Circuit Affects the Frequency of Oscillation
- As you can see in the below figure the input impedance of the amplifier behaves as a load on the resonant feedback circuitry and decreases teh Q point of circuitry.
- The resonant frequency of parallel resonant circuitry relies on the Q according to this below formula.
fr= 1/2π√LCT√Q2/Q2+1
- if the value of Q is greater than ten the frequency values is almost according to given relation.
fr=1/2π√LCT
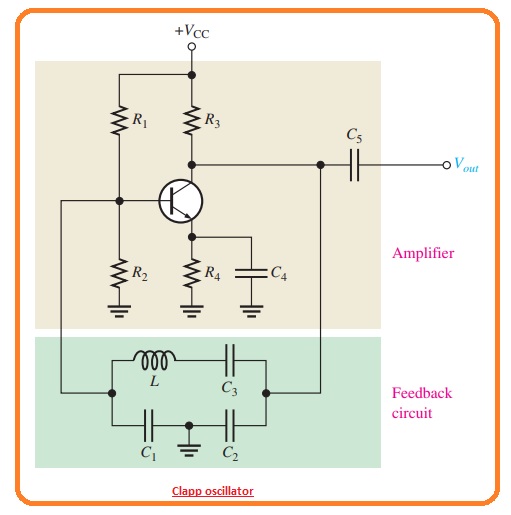
What is Clapp Oscillator
- The Clapp oscillator is some change in the circuit of Colpitts. The main difference is an extra capacitor is a need in series combination with the inductor in the resonant feedback circuitry. as can be seen, in below figure.
- As the capacitor C3 is in series combination with the capacitor C1 and C2.
- So-net capacitance will be.
CT=1/(1/C1+1/C2+1/C2)
- The net frequency of oscillation is Q>10
fr=1/2π√LCT
- If eh value of C3 is less than the value of capacitor C1 and C2 then c3 capacitor completely controls the resonant frequency. As the capacitor, C1 and C2 are linked with he ground terminal through one end the junction capacitance of the transistor and other stray capacitances look in parallel combination capacity c1 and C2 and with eh ground.
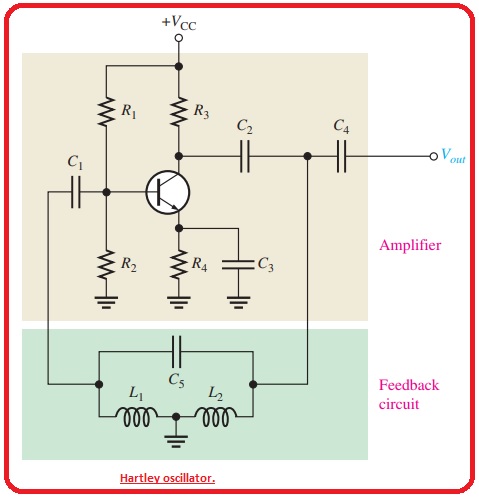
Hartley Oscillator
- The Hartly oscillator circuit combination is like to the Colpitts with the difference is that feedback circuit comprises of 2 series inductors and parallel capacitor shown in the below figure.
- In this circuitry, the value of oscillation frequency for Q>10 is given as.
fr=1/2π√LCT
- Here LT=L1 +L2. Inductor behaves in action like to the capacitor c1 and C2 in the colpitss to find the attenuation of the feedback circuitry.
B=L1/L2
So friends that is a detailed post about Operation of LC Feedback Oscillators if you have any further query ask in comments. Thanks for reading. Have a good day.