As matrix theory is not only the cornerstone of just math and statistics, but also a strong foundation of almost all disciplines. There are numerous uses of matrices theory in all these disciplines which includes math, finance, economics, statistics and applied sciences. There are many other applications of linear algebra in practical life but for the time being we have discussed its applications in applied mathematics.

Matrix theory and its application in Applied Mathematics:

The construction of mathematical models while solving systems of equations is one of the most common applications of matrix theory in Applied Mathematics. We will discuss all applications in detail.

1. Phoet al in 2018, studied the algorithm of newton and proposed the function of Max link. This technique had several applications in statistics and models of regression for missing data.
2. In 2019, various newton methods regression models being used in decision sciences and education used matrix theory.
3. Optim, Nleqslv used matrix theory to determine parameters in many regression models, which are useful functions in R programmed by the newton method.
4. Furthermore, the moment generating function, expectation, and variance of ubiquitous distribution with applications in decision sciences. Pho et al reviewed the four optimal solution methods in decision sciences; bisection, gradient, secant, and newton methods.
5. On the other hand, Song et al. reported the Cramer rule for the unique root of restricted matrix equation over the quaternion skew fields, whereas JI introduced explicit formulas of the generalized inverses and condensed Cramer rule.
6. EEvibes is an online teaching website where you can find many courses related to electrical engineering. Also you can find complete course of linear algebra there.

Developing of financial models:

1. The theory of matrix was combined with the theory of cost of capital developed by Wong and Chan (2004). A pseudo Bayesian model was created that can explain investor behavior and market anomalies such as under and overreaction, as well as market volatility.
2. Matrix theory was also used to expand the cost of capital theory to a time series model that gives dividends.
3. The spectrum theory of big dimension any matrices and its application to wireless communication and finance statistics

  Creation of economic models:

1. Lewis and Thorbecke in 1992 reported findings from a low regional social accounting matrix on district-level economic links of Kenya. The relevance of revenue was emphasized for sharing local economic impacts of renewable energy project. This approach is known as social accounting approach.
2. A social accounting approach illustrated economic and environmental efficiency using the theory of matrix.
3. Masseti developed a social entrepreneurship matrix as a “tipping point” for economic change.
4. In an economic review of rheumatoid arthritis, a matrix of cost domains was proposed. Random matrix theory and the failure of macroeconomic projections were also introduced by Mounfield.
5. Wong and Ma extended their work on the theory of indifference curve to incorporate the location-scale family in a multivariate context for risk averters and risk seekers. This idea could be readily implied.
6. In a multivariate situation, investor with reverse S-shaped utility functions developed a new statistics frontier model using matrix theory and its depiction.

  Creation of statistical models:

1. The random matrix theory and universal statistics of chaotic quantum wires introduced the random matrix theory of chaotic quantum wires with spin-dependent hopping and the universal statistic.
2. Searl introduced the algebra of matrices for help and understanding in statistics.
3. Andrew developed spectral statistics using the theory of large sample form of matrices. It was further developed by introducing spectrally right estimates.

1. The stochastic dominance (SD) for averters and seekers were evolved and carried out through the concept of matrix theory concept to broaden SD checks for hazard averters and seekers.
2. The SD theory for buyers with reverse S-formed application capabilities broadened and evolved by the concept of the matrices.

  Applications of mathematical, economical, financial, and statistical models:

After using the matrix theory to develop mathematical, economical, and financial models ad discussed above, we might consider using the model to analyze the real-life problems.

1. For instance, after using a random matrix theory in developing portfolio modeling models. Many people have used portfolio improvement theory to go through financial issues of interest.
2. There are some useful uses of work after applying the theory of matrix for example in the production models, risk measures, cointegration and causality and certain domains.
3. In terms of economical quality, it worked on technical analysis, trading techniques and calendar anomalies.
4. There are many uses in financial stocks also. For instance, warrant markets, stock markets, currencies and housing marketing.
5. The theory of matrix is also being used in marketing techniques and management.

Application of Matrix Theory in Education:

Matrix theory plays a vital role in the field of education. Following are some application of matrix modeling:

• Mathematical modeling capabilities for high school teachers.
• Capacity of mathematical modeling for high school students.
• Effective way of teaching through mathematical modeling.

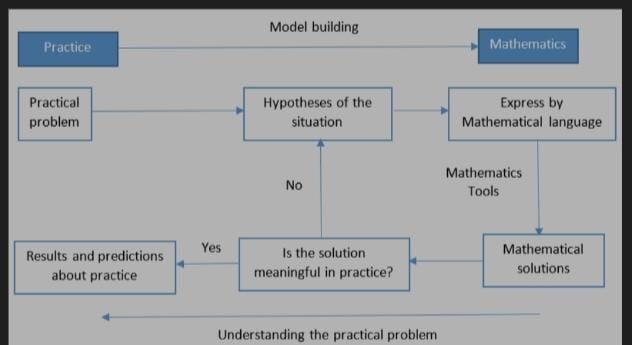
        Mathematical Modeling Steps:

• selection of an unknown variables is our first step.
• Then select the condition for the variable.
• Solve the equation
• Checking the solution is also a compulsory step

Application of Matrix Theory in Reality:

The National student mathematics Olympiad is a very important examination for university students in Vietnam because the contest gives a good motive to students for learning and improves the teaching quality as well.

Practical mathematics problems in the national student mathematics Olympiad

Problem:

Let a and b be real numbers in any matrix A.

Solution:

• Find the determinant of A
• Compute A^-1
• A is invertible
• Find the values of a and b

Solving problems:

• Find determinant
• If a is not equal to b then A is invertible
• Then use crammer rule
• Then apply system of linear equations
• Then solve the equations

Conclusion:

So from the above discussion the matrix theory plays a very important role in teaching mathematics and this theory is so helpful in field of economics, engineering, sciences and finance etc.