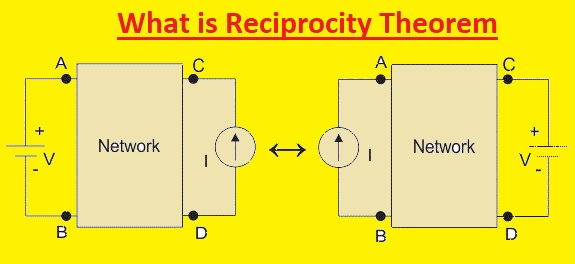
 Hello, readers welcome to the new post. In this lesson, we will learn What is Reciprocity Theorem. Reciprocity in the electrical system is a feature of circuitry that makes the relationship between volts and current at two points of the circuit. This thereon explains that the current at one point of the circuit due to the other point voltage is the same as the 2nd point current due to voltage at the first point.
Hello, readers welcome to the new post. In this lesson, we will learn What is Reciprocity Theorem. Reciprocity in the electrical system is a feature of circuitry that makes the relationship between volts and current at two points of the circuit. This thereon explains that the current at one point of the circuit due to the other point voltage is the same as the 2nd point current due to voltage at the first point.
This theorem is applicable to all types of passive circuits. Reciprocity theory is characteristic of the principle of reciprocity in electromagnetism. In this post, we will discuss this theorem works and solve practical examples. So let’s get started
Description of Reciprocity Theorem
- The voltage source and ammeter used in the circuit where the reciprocity theorm has to apply must be ideal. In other words, the inner resistance value of the ammeter and voltage source be zero. The reciprocal circuitry can simple or complicate the system. So during the application of complicated reciprocal passive circuitry can be converted in a simple network. In the case of a linear passive system voltage V and output current can be transferred. The ratio between voltage and current is called transfer resistance.
How to Apply Reciprocity Theorem on Electrical Network
- There are some steps involved to solve networks through the use of the reciprocity theorem.
- First of all, select the branches of circuitry where the reciprocity theorm has to apply.
- To find the value of current flowing in breach any circuit analysis technique like KVL, KCL, etc can be applied
- In the next step interchanged the voltage sources between branches that we choose in the first step
- Now find the current in the branch that has a voltage source before the reciprocity application
- Now we can see that the current calculated in step two and the current find in step four where sources are interchanged have same value
Reciprocity Theorem Example with Solution
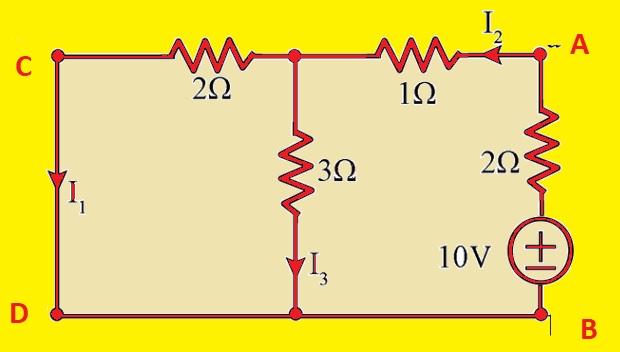
- Now we solve the circuit and apply the reciprocity theorem.
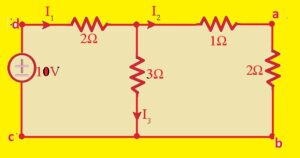
- If we solve the above circuit and find the equivalent resistance value across the points C and D then we have
- Req= [(2+1)II3]+2= 3.5 ohm
- If we use this equivalent resistance and find the current I1
- 10/3.5= 2.86A
- Now I2
- I2=2.86 x3/(3+3)=1.43A
- Now find I3
- I3=2.83-1.43= 1.43A
- Now solve other circuits
- In this circuit voltage source is on the right side while the first circuit has on the left side.
- If we solve for an equivalent circuit then we have
- Req=(2II3)+1+2= 6/5+3=21/5=4.2ohm
- Find I2=10/4,2=2.381A
- Then we have I1=I2(3/(3+2)=2.381×3/5= 1.43A
- So from these two circuitry solutions, we can find that the branch that has a source has a current 1.43 A in the first circuit and in the second circuit, the branch that has a voltage source also has a 1.43A current. So we have provided the reciprocity theorem
Where is the reciprocity theorem used?
- This theorem is used for AC and DC circuits solution. In simple words reciprocity, theory explains that when the position of any voltage and current sources in circuits is changed then the same value of current and volts will flow before and after interchanging
What are the limitations of the reciprocity theorem?
- The limitation of this theorem is that it is used to circuits that have one source and is not applicable for multiple source systems. The system where this theory has apply must be linear and have resistances, inductors, capacitors, and compiled circuits. It not applicable for circuits that have time-varying components
Is reciprocity theorem valid for both DC and AC circuits?
- It is applicable to AC and Dc circuits
Whether Antennas will satisfy the Reciprocity theorem?
- Antennas satisfy the reciprocity theory. So this theorem can be used for transmission antenna or receiving antenna
That is all about the Reciprocity Theorem. All details have been explained. IF you have any queries ask here