Torque Induced in a Current-Carrying Loop

Hello fellows, I hope all of you are fine. In today’s tutorial, we are gonna have a look at Torque Induced in a Current-Carrying Loop. Different kinds of motors are finest examples of current-carrying coils in a field. An electric motor has rotor windings when place in an exterior field which is in the case of motors is a field of the stator. When current flows through the windings of a rotor or loop there is another field in the rotor which relates to the field of stator and torque produced in the rotor which rotates this motor. By this method, electric power transformed into mechanical.

It today’s post we will explain the torque induced in the simple loop which is put in the field then relate loop findings with the different AC machines. I also have written an article on the A Simple Loop in A Uniform Magnetic Field you should also study this before understanding the torque induced in the loop. So let’s get started with Torque Induced in a Current-Carrying Loop.

Torque Induced in a Current-Carrying Loop

• In the last tutorial The Voltage Induced in a Simple Rotating Loop we discuss the rotation of the loop in the field and calculate the voltage induced in it.

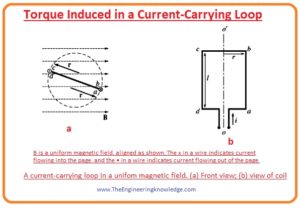
• Now let’s suppose that if a loop is rotating in the field at some angle θ, then the current passing the loop is shown in a given diagram.

• If the current is passing in the loop then there will be torque induced in the loop.
• To find how much torque will be produced in the loop see a given diagram explaining the torque at each side of the loop.

• The force working on every side of loop will be given by this equation.

F =I (l x B)

• • In this equation
  • F is the force working on the sides.
  • I is the current at the correspondent side.
  • L is the length of the side.
  • B is the field in which loop is rotating.
• The applied torque on any side will be found by the given equation.

T = (force applied) x (perpendicular distance)

= (F)(rsinø)

= rFsinø

• In this equation, ø is the angle between the r and the force (F).
• The direction of torque will be clock-wise if it rotates machine in the clock-wise and its direction is in anticlockwise if it rotates machine in anticlockwise.
• Now we find the torque at each side of the loop and will add them to find the total torque in the loop.

Torque at side ab:

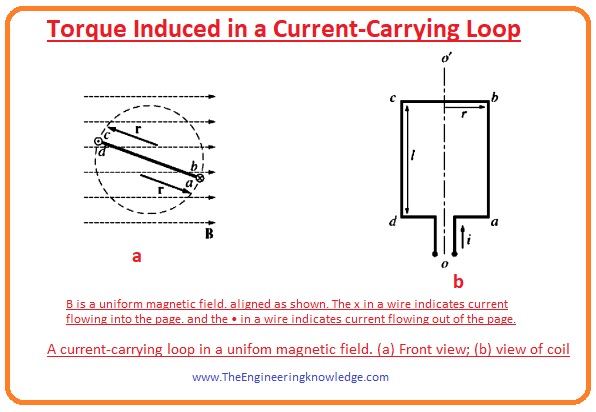
• At this side, the direction of current is into the page but the direction of field is toward right it is denoted as A in a given diagram. So, the (l x B) direction will be downward. So, the force applied on this side will be.

F =I (l x B)

= ilB downward direction

• so the resultant torque at side ab will be given as.

t_ab= (F) (rsinø_ab)

= rilBsinø_ab clockwise

Torque at side bc:

• At this side, the current points towards the plane of the page, and the field direction is towards right. Its denoted as (B) in the figure. The direction of the term (l x B) is toward the into the page. So the force applied on side bc is given as.

F= i(l x B)

ilB into the page

• The torque at the side bc will be zero because the vector r and l are parallel to each other both of these two have direction into the page and the angle (ø_bc) is zero.

t_bc= (F) x (rsin ø_bc)

= 0

Torque at side cd:

• At this side the current flowing out of the page, but the field direction is towards right. It denoted in figure as C. the direction of the term (l x B) is toward up.
• So the force on this side will be.

F = i(l X B)

ilB up

• The correspondent torque at this side given as.

t_cd = (F) (rsinø_cd) clockwise

Torque at side da:

• At this side, the current is flowing in the page, but the direction of field is toward right. It denoted in figure as D.

• The direction of the term (l x B) is out of the page. The force at this side is given as.

F =i(l x B)

ilB out of the page

• On this side the torque is zero because the as the vector r and l are parallel to each other the ø_da is zero.

t_da = (F)(rsinø_da)

= 0

• The total induced torque on the loop will be sum of the torque at every side.

t_ind = t_ab + t_bc + t_cd + t_da

= rilBsinø_ab +rilBsinø_cd

• Not that ø_ab = ø_cd so the total induced torque will be

t_ind =2rilBsinø —–(1)

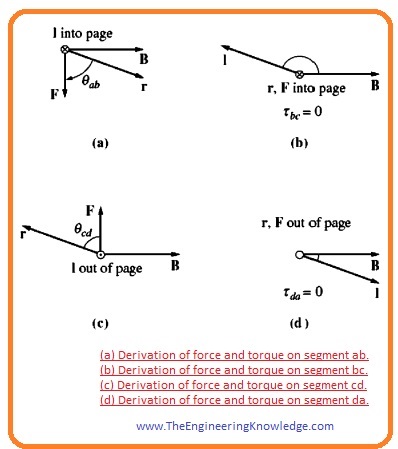
• The corresponding torque according to this equation is shown in a given diagram.

• You can see that the torque value of torque is at extreme point when loop’s plane is parallel with the field, and torque is 0 when the loop’s plane is 90 degrees to the field.
• There is another method to explains the equation (1), which compares the behavior of the loop with the different AC (Alternating Current) machines.
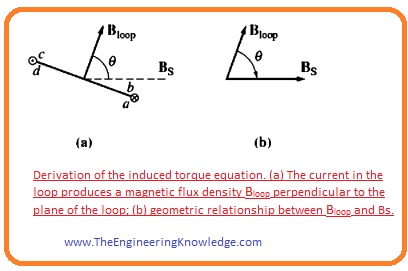
• To find this other method or expression we study a given diagram.

• If the current moving in the direction as drawn in give a figure. This current will produce field in the loop the direction of field (B_loop) generated is shown in a given figure.
• The magnitude of the field generated will be.

B_loop = (ui/G)

• In this equation G depends on the geometrical shape of the loop and area of this loop is 2rl because of it like the rectangle.
• By putting the value of (B_loop) and area of a loop in the equation (1) we have a new equation of torque.

t_ind = (AG/u ) (B_loopB_ssinø)

• In this new equation (AG/u ) is constant which depends on the physical parameters of loop.

t_ind=K(B_loopB_ssinø)—(2)

• In this equation, B_s is the field of stator and ø is the angle between B_loop and B_s.
• The direction and magnitude of produced torque can be written as the cross product.

t_ind= KB_Loop x B_s

• From this equation, we can conclude that the induced torque in the loop is directly proportional to the field induced in the loop, external field, and the sin of the angle between these two fields.
• This torque induced principle also like the torque induced in the AC machines.
• In a simple way above given details, we can conclude that torque induced in any AC machine depends on the 4 factors which are described here.

1. 1. The field of the rotor.
   2. The field of external part (stator).
   3. The sin angle among stator field and the rotor field.
   4. The fourth one is constant (K) it is the physical parameters of machines.

That all bout the torque induced in a loop I have mentioned each and everything related to it. If you still have any questions about it ask in comments. See you in the next tutorial.