Kinematic equations are mechanical system equations, like those of a robot manipulator, that define motion at one or more points to obtain the required functions. The main features of kinematics equations enable the analysis and design of systems, such as 4-bar linkages, as well as serial and parallel robots.
These equations define the link rigidity and joints that give rotations. In this post, we will cover details for kinematic equations and their practical application.
What is kinematics
- Kinematics is a branch of physics that explains motion according to time and space without considering its main cause.
- Kinematics equations are equation sets that help measure unknown aspects of body motion along with other factors.
- Commonly used kinematics variables are
- Displacement (Δx)
- Initial Velocity (v₀)
- Constant acceleration (a)
- Final Velocity, v
- Time interval (t)
Kinematics equations help to find one or more of these variables with other measured values. These equations explain motion at constant velocity or with constant acceleration.
Since kinematic equations apply for constant speed or constant acceleration, they are not used for changing factors.
Definition of Inverse Kinematics:
- inverse kinematics: Perform the reverse function of kinematics. Basically, the inverse kinematics process involves the measurement of joint angles used for the robot to get the required direction.
Kinematics Basics
Read also Difference Between Kinematics & Kinetics
Kinematics is employed for finding the velocity, locations, and acceleration of objects. In kinematics, forces do not have high importance, so they are not considered high.
Position
- Position defines the locations of objects. It is defined in the form of coordinate points, x, y, z, etc. change in position called displacement. It is denoted as Δx, Δy, and Δz.
- displacement measured in meters
Velocity
- Velocity defines body speed in a certain direction. Its measuring unit is meters per second. The rate of change of displacement is called velocity. Uniform velocity has the equation v=Δx/Δt.
Acceleration
- Acceleration defines velocity change with time. It is measured in m/s² or meters per second squared.
- For uniform acceleration, the equation is a=Δv/Δt.
What are the Kinematic Equations?
- Kinematics equations define the motion of a body with constant acceleration. Kinematics equations use rate of change, derivatives, and integrals for finding solutions.
- The applications of kinematic equations are the use of specific notation for showing initial and final values. such as if we have an initial velocity, V₀, and final velocity, V.
- Change in velocity is denoted in equation form as ΔV ΔV= V-Vo.
- This notation is also applicable to time and displacement. X₀ is the initial position, x is the final position, and t₀ is the initial time, and t is the final time.
- 4 main types of kinematics equations are
Kinematic Equations
v=v0+at
Δx=(v+vo)/2.t
Δx=vot+1/2at^2
v^2=v0^2+2aΔx
Let’s explain each equation one by one
First Kinematic Equation
v=v0+atv=v0+at
- In this equation, the final velocity is equal to the initial velocity with acceleration multiplied by time.
- If we have constant acceleration for some time, we will get final velocity.
- This equation is used when changes in velocity exist with constant acceleration.
Third Kinematic Equation
Δx=vot+1/2at^2
- This equation is defined as displacement equals initial velocity multiplied by time plus half of acceleration squared.
- displacement related to initial velocity and constant acceleration without finding the final velocity.
- This equation is used for measuring final velocity.
- The other form of the second kinematic equation is as
x=x0 + v0t + 1/2at^2
- It looks different; the basic difference is that it splits Δx into x−x₀x−x₀ and then solves to get Δx on its own.
- This version is used for the final or initial position rather than displacement.
Fourth Kinematic Equation
v^2=vo^2+2aΔx
- • The fourth kinematic equation is defined as final velocity squared equal to initial velocity squared plus double acceleration times displacement.
- This equation does not involve time.
Rotational Kinematics Equations
image from this equation https://byjus.com/physics/kinematics-equations/
- Above, we discuss translational or linear kinematics equations that work for motion and linear movement of objects. Kinematic equations also have another branch that work with the rotational motion of the body.
- That comes with some variable changes.
- change in angle used for displacement
- Initial and final velocity are replaced by initial and final angular velocity.
- acceleration replaced by angular acceleration
- Time is constant.
How to choose the Right kinematics Equation?
- Kinematics equations are used for solving different dimensional motion equations that work with the motion of objects with constant acceleration.
- For solving any problem, the selected equation needs to have an unknown variable and also three known variables.
- equations needed to miss one variable. In this way, we can find the missing variable in the equation.
- Before equation selection that does not have missing variables, check these factors.
displacement missed
- This equation does not have Δx and is used for solving questions that are not discuss displacement.
V=Vo+at
Missing acceleration
- This formula is used for questions that do not involve acceleration. But in some conditions, acceleration is indirectly referenced, like if an object is in a free-fall state.
Δx= (V+Vo)/2. t
Missing final velocity
- This equation uses equations that do not have a final velocity. In some conditions,the final velocity is indirectly referenced. for questions where the term “before stopping” is used, use the quadratic formula for problem-solving.
Δx=Vot+1/2at^2
Missing time
- If the equation does not have a time interval, this equation is used
V^=Vo^+2aΔx
How to Derive the Kinematics Equations
First Equation:
- First of all, start considering the acceleration formula that says
a=ΔV/Δt
- As we know, ΔV=V-vo, and using it in the above equation, we have
- a=(V-vo)/Δt
- Solving the above equation, we get the value of V as
V=Vo+aΔt
- If denotes a time interval as t then the equation becomes
V=Vo+at
Second Equation derivation
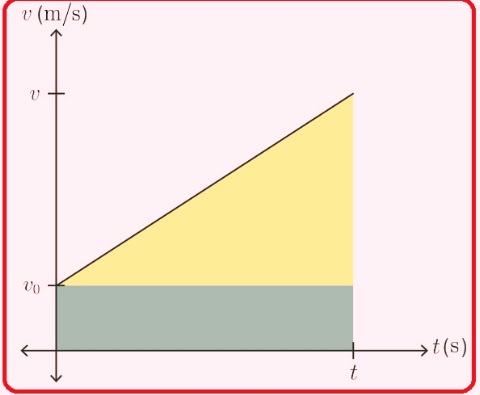
- For deriving this equation, we will use a velocity-time graph where acceleration is constant. The velocity-low graph is defined as acceleration, and the area below the graph defines displacement.
- The height of the green rectangle is Vo, and the width is denoted as t, so the area is Vot.
- The base of the yellow triangle is denoted t and the height is v-vo; the yellow triangle area is
1/2 t(v-vo)
- Through the addition of yellow and green areas, we will get
Δx=Vot+1/2t(v-vo)
- disturbing factor 1/2t we will get,
- Δx=Vot+1/2tv-vo1/2t
- Second kinematic equation
- Δx=(v+vo)/2.t
Third Equation:
We find the 3rd kinematic equation by using the first kinematic equation in 2nd equation
- First, use the second kinematic equation
- Δx/t=(v+vo)/2
- using the first equation for v in the second equation
- V=Vo+at
- After putting, we will get
- Δx/t=(Vo+at+vo)/2
- Further expanding we will get
- Δx/t=(Vo/2+at/2+vo/2)
- Δx/t=vo+at/2
- By multiplying the above equation by t we will get
Δx=vot+at^2
Fourth Equation:
- 4th kinematic equation derived with the help of first and 2nd kinematic equations
- First use the formula
- Δx=(v+vo)/2.t
- first we use the first kinematic equation
- V=Vo+at
- t=(V-Vo)/a
- We use this formula in the above equation to get,
- Δx=(v+vo)/2.(V-Vo)/a
- Taking the multiplications of the above values
- Δx=(v^2-vo^2)/2a
- Solving the equation for v^2 we get
- v^2=vo^2+Δx2a
Kinematic Equations examples
Read also What is a catalytic converter? Features, Working, Uses
Example 1 equation: Finding Final Velocity
- A car accelerates from rest at 3.0 m/s for 5.0s. What is its final velocity?
Given:
v0=0 m/s
a=3.0 m/s^2
t=5.0 st = 5.0s
Using equation
v=v0+atv
v=0+(3.0)(5.0)=15.0 m/s
V= 0 + (3.0)(5.0) = 15.0
Example equation 2: Finding Displacement
Using the same car, find the displacement in 5 seconds?
Given:
v0=0 m/s
a=3.0 m/s^2
t=5.0 s
Using Δx=v0t+1/2at^2
Δx=0+1/2(3.0)(5.0)2=37.5 m
Example equation 3: Solving Without Time
A rock is thrown upward at v0=20.0 m/s. What is the maximum height it reaches? ( a=−9.8 m/s^2, and at the top, v=0 m/s
Using
v^2=v0^2+2aΔx
0=(20.0)^2+2(−9.8)Δx
Δx= 400/19.6=20.4
The rock reaches a height of 20.4 m.